- 加速度の定義
- \(v=v_0+at\)の証明
- \(S=v_0 t+\frac{1}{2}at^2\)の証明
- \(v^2-v_0^2=2aS\)の証明
- \((v-t)\)図の性質
- \((v-t)\)図を用いた3公式の証明
- 3公式の使い方
加速度の定義
公式を覚える前に物理量の定義はしっかりと覚えて欲しいです。加速度の定義は単位時間当たりの速度変化です。例えば、\(\Delta t \)[s]間で速度が\(\Delta v \)[m/s]変化したとします。このとき,加速度\(a\)は次のように表すことができます。
$$a=\frac{\Delta v }{\Delta t } $$
\(v=v_0+at\)の証明
ここで,時間\(t\)[s]の間に速度が\(v_0\)から\(v\)に変化したとします。このとき,速度変化\(\Delta v \)は\(v-v_0\)と表せるので加速度\(a\)は、
$$a=\frac{\Delta v }{\Delta t } =\frac{v-v_0}{t-0} $$
と表せます。これを式変形した以下の式が,3公式の1つ目の式となります。
$$v=v_0+at \tag{1}$$
\(S=v_0 t+\frac{1}{2}at^2\)の証明
次に,\(\ t \)[s]間での位置変化(変位と言い,\(\ S \)で表します)を求めましょう。中学では移動距離を\(速さ\times時間\)で求めました。しかし,加速度運動をしているので速さが一定ではありません。そこで,速さの平均値\(\ \overline{v} \)を考えます。時刻\(\ 0 \)[s]と時刻\(\ t \)[s]での速さの平均を考えると,
$$\ \overline{v}=\frac{v_0 + v }{2} $$
となります。これより,\(\ t \)[s]間での変位\(\ S \)は,
$$\ S=\overline{v}\times t=\frac{v_0 + v }{2}\times t $$
となります。ここで,先ほど導出した\(\ v=v_0+at \)を用いて式変形すると,
$$\ S=\frac{v_0 + v_0 +at }{2}\times t=v_0 t+\frac{1}{2}at^2 $$
となり,等加速度運動の2つめの公式を導出することができました。
$$S=v_0 t+\frac{1}{2}at^2 \tag{2}$$
\(v^2-v_0^2=2aS\)の証明
等加速度運動の3公式(1)(2)で以下の2つの式を導出しました。
$$\ v=v_0+at \tag{1}$$
$$\ S=v_0 t+\frac{1}{2}at^2 \tag{2}$$
3つ目の式は(1)(2)の2式から\(\ t \)を消去するだけです。
\(\ t \)の次数が少ない(1)式から\(\ t \)を求めます。
$$\ t=\frac{v – v_0}{a} $$
これを(2)式の\(\ t \)に上で求めた\(\ t \)を代入します。
$$\ S=v_0 \frac{v – v_0}{a} + \frac{1}{2} a (\frac{v – v_0}{a})^2$$

こんな計算、難しくてできません!

それでは次の方法はどうでしょうか?
(2)式を導出した際に、速さの平均と時間をかけることで変位を出しました。このときの式に\(\ t \)を代入してみましょう。
$$\ S=\frac{v_0 + v}{2}t=\frac{v_0 + v}{2}\frac{v – v_0}{a}=\frac{v^2 – v_0^2}{2a}$$
これを整理すると3つ目に式を導出することができます。
$$v^2-v_0^2=2aS \tag{2}$$
\((v-t)\)図の性質
等加速度運動の問題はグラフを描くことでイメージしやすくなります。\(\ (v-t) \)図の性質を考えてみましょう。
図傾き.gif)
グラフの傾きは\(\frac{(縦軸の変化量)}{(横軸の変化量)} \)で定義されています。等加速度運動の3公式(1)~(3)でも出ましたが、変化量を表す記号は\(\Delta \)です。例えば\(\Delta x\)は「\(\ x \)の変化量」を表しています。グラフの横軸が\(\ t \)、縦軸が\(\ x \)なので、
$$ (傾き)=\frac{(縦軸の変化量)}{(横軸の変化量)} =\frac{\Delta x}{\Delta t}=(加速度)$$
となり、\(\ (v-t) \)図の傾きは加速度を表していることが分かります。
次に、グラフの面積について考えてみます。次の図の斜線部分に注目してみましょう。
図変位1.gif)
この面積はある時刻で、非常に短い時間\(\Delta t\)の間に進んだ距離(変位)を表しています。時間によって速度が変化するので、各時刻での変位を足し合わせたものは次の図の斜線部分になります。
図変位2.gif)
図変位3.gif)
これより、\(\ (v-t) \)図の面積が変位を表していることが分かります。
\((v-t)\)図を用いた3公式の証明
等加速度運動の3公式を(1)~(3)で証明をしました。今回は\( (v-t) \)図の性質を用いて証明していきましょう。次のようなグラフを考えます。
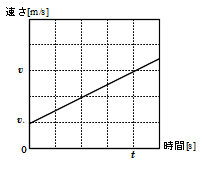
\( (v-t) \)図の傾きが加速度\( a \)に等しいことから、
$$\ a=\frac{v-v_0}{t-0} $$
となります。これを式変形することで3公式の2つ目の式を導出できます。
$$\ v=v_0+at \tag{1}$$
次に、\( (v-t) \)図の囲む面積が変位\( S \)に等しいことから、
$$\ S=\frac{1}{2}(v_0+v)t $$
となります。(1)式を用いて式変形すると3公式の2つ目の式を導出できます。
$$\ S=v_0 t+\frac{1}{2}at^2 \tag{2}$$
(1)式と(2)式を用いてを消去すれば、3公式の3つ目の式を導出できます。
$$v^2-v_0^2=2aS \tag{3}$$
(計算方法はコチラから確認して下さい。)
3公式の使い方
今回は等加速度運動の3公式の使い方についてです。それでは以下の問題を解いてみましょう。
コチラをクリックすると新しいタブを開いて問題を見ることができます
02-7-1
解答を始める前に3公式を使うポイントを説明します。次のことが一番大事になります。
慣れるまでは「○向き正」というように、正の方向を決めておくことをお勧めします。
(1)
速度を求める問題なので\((v=v_0+at)\)を使います。初速度の方向を正として、\((v=v_0+at)\)より、
$$ 10+(-5)\times 1.0=5.0$$
答えが正になっているので、初速度の方向に5.0[m/s]となります。
(2)
変位を求める問題なので\((S=v_0 t+\frac{1}{2}at^2)\)を使います。初速度の方向を正として、\((S=v_0 t+\frac{1}{2}at^2)\)より、
$$ 10\times1.0+\frac{1}{2}(-5.0)(1.0)^2=7.5 $$
答えが正になっているので、初速度の方向に7.5[m]となります。
(3)
折り返し地点では物体の速さが0になるので、求める時刻を\(t\)、初速度の方向を正として、\((v=v_0+at)\)より、
$$ 0=10+(-5.0)t \\ ∴ t=2.0 $$
となります。これより、答えは2.0[s]となります。
(4)
元の位置に戻ることになるので変位が0となります。求める時刻を\(t’\)、初速度の方向を正として、\((S=v_0 t+\frac{1}{2}at^2)\)より、
$$ 0=10t’+\frac{1}{2}(-5.0)t’^2 \\ \leftrightarrow t'(t’-4)=0 \\t’=0,4 $$
0[s]は最初の位置なので、答えは4.0[s]となります。また、初速度の方向を正として、\((v=v_0+at)\)より、
$$ 10+(-5.0)\times 4.0=-10 $$
答えが負になっているので、初速度の方向と反対向きに10[m/s]となります。
(5)
最後は「道のりの長さ」を求める問題なので、これを直接求める式はありません。初速度の方向を仮に右とすると、この問題では右に進んでから折り返し、左に進んで戻って来ています。ですので、折り返すまでに右に進んだ距離と折り返してから元の位置に戻るまでに進んだ距離を足したものが「道のりの長さ」になります。折り返すまでに進んだ距離は初速度の方向を正として、\((S=v_0 t+\frac{1}{2}at^2)\)より、
$$ 10(2.0)+\frac{1}{2}(-5.0)(2.0)^2=10 $$
となります。元の位置に戻っていることから、右に進んだ距離も左に進んだ距離も等しいので,道のりの長さは20[m]となります。
等加速度運動についてはこれで終了します。他には、グラフを使った解法や\((v^2-v_0^2=2aS)\)を使った解法などがありますが、詳しくは問題集や解説を参考にしして下さい。なお、「\((v=v_0+at)\)より」というのは問題を解くときには必ずノートに書くようにして下さい。文字式計算ならともかく、今回のような数値計算では何をしているのかが分からなくなってしまいます。それに、「\((v=v_0+at)\)より」と毎回書くことで公式を覚えるのではなく身につける(自然と覚えてしまう)ことができます。次は「落体の運動」に入ります。頑張りましょう!